HJF Python

数据类型#

1 基础数据类型#

1.1 数值类型#

用于存储数字值，根据数值特点分为三类：

整数（Int）
- 表示任意大小的整数，支持十进制、二进制（以 0b 开头）、八进制（以 0o 开头）、十六进制（以 0x 开头）表示。
- 特点：上不封顶，3.8 以后建议使用 = 代替 is 比较整数。
浮点数（Float）
- 表示小数或科学计数法表示的数（如 1.23、4.5e-6）。
- 特点：存储为双精度浮点型（64位），可能存在精度误差和截断误差，精确到 15 位十进制小数
复数（Complex）
- 由实部和虚部组成，格式为 a + bj（a 为实部，b 为虚部，j 表示虚数单位）。
- 特点：适用于科学计算和工程领域中的复数运算。

1.2 布尔类型（Bool）#

仅有两个取值：True（真）和 False（假）。
and, or, not, != 分别是且、或、非、异或
or, and 为短路运算，并不强制返回布尔值，但是非和异或返回的是布尔类型
类型可以自定义 __bool__ 方法来控制布尔值的返回，默认 len()==0 对应 false ，其他 true

1.3 python 中的对象#

每个对象有唯一的标识码，可以通过 id() 函数获取，是该对象的内存地址，使用 is 比较两个对象是否相同。

2 序列类型#

列表 list，元祖 tuple，range
字符串 str
字节流类型

2.1 列表（List）#

不同类型可以混在一起
实际存放的是引用对象
下标访问为按引用取值
赋值是指向新的对象

常用方法

增 append
插入 insert
查找、定位：index

2.2 元组（Tuple）#

一旦初始化后不可更改
其中嵌套的元素可变，如果嵌套的是列表就可以修改列表
解包：c, d, *_ = a，合并直接用 +

2.3 string#

可读、可下标访问、不可修改
反斜杠用法与 C 语言一致
.strip() 返回一个新的对象
count 函数是 find 函数的复用
拆分、合并用 split()、join()

2.4 迭代器#

语句块 for 不会产生独立的命名空间
迭代器可以作用于 for 循环，也可以被 next() 函数调用
列表生成式 [x for x in iterable] 返回一个列表
生成器表达式 (x for x in iterable) 返回一个迭代器

2.5 set 集合#

{} 表示集合
使用 set() 完成类型转换

2.6 字典（Dict）#

无序、可变的键值对集合，用 {键: 值} 格式定义。
键必须是不可变类型（如字符串、数字、元组），值可以是任意类型。

2.7 容器类#

容器（container）类（如：list，string，set，tuple，dict…）都内建有一个操作函数来返回一个迭代器（iterator）。该迭代器被用来支持 for循环语句，以及in操作。同时还支持.next()接口，返回下一个对象。
字典可以用关键字遍历

2.8 列表生成式#

嵌套的列表生成式

2.9 高阶函数#

map，reduce，filter

3 第一次作业讲评#

python 3.13 对于 // 的处理方式等于先 / 再算 floor
同一函数的默认参数会指向同一个数据体，不论其类型以及是否可变
列表乘法的本质是创建了对同一个列表进行引用的复制而不是多个列表，但是注意如果修改的是不可变对象，则不会有影响

函数编程#

解包再 zip 等价于转置

1 对象拷贝机制#

加赋值引用并不会直接导致对象被复制

对象复制和对象引用的复制
浅拷贝：copy.copy()，只复制对象本身，不复制对象包含的子对象。
深拷贝：copy.deepcopy()，创建一个新对象，然后递归地插入原始对象中元素的拷贝
list 的切片操作会生成新的对象，但实际上只有一层复制而已

2 名字绑定及引用计数#

sys.getrefcount() 函数可以获取对象的引用计数，注意在函数调用时会增加一次引用计数。

3 函数的一般性质#

参数传递的本质是传递对象引用而非对象副本，返回值也是对象引用

4 函数实现generator#

使用 yield 关键字创建生成器函数，返回一个迭代器对象。
生成器函数可以派生出多个生成器示例，相互独立

5 匿名函数（Lambda表达式）#

用于创建简短的一次性函数，语法：lambda 参数: 表达式。常见用途：作为参数传递给高阶函数（如 map、filter）。

6 函数高阶使用技术#

6.1 可变参数列表#

使用 *args 接受任意数量的位置参数，返回一个元组。
使用 **kwargs 接受任意数量的关键字参数，返回一个字典。

6.2 嵌套函数#

在函数内部定义另一个函数，内部函数可以访问外部函数的变量。
变量的作用域：python 引用变量的顺序
1. 局部作用域（函数内部）
2. 闭包作用域（嵌套函数）
3. 全局作用域（模块级别）
4. 内建作用域（内置函数和变量）
不声明就是局部变量，nonlocal 声明可以访问外部函数的变量，global 访问全局变量
函数闭包：内部定义了一个函数，把该函数作为返回值

6.3 函数装饰器#

装饰器是一个函数，用于在不修改原函数代码的前提下，增加额外功能。
装饰器语法：@decorator_name，放在函数定义前。
装饰器可以嵌套使用，也可以接受参数。
所有被装饰的函数实例共享同一个公共缓存，可以实现记忆化存储

7 文件操作#

open() 函数用于打开文件，返回一个文件对象，完整定义是 open(file, mode='r', buffering=-1, encoding=None, errors=None, newline=None, closefd=True, opener=None)。
mode 可选值
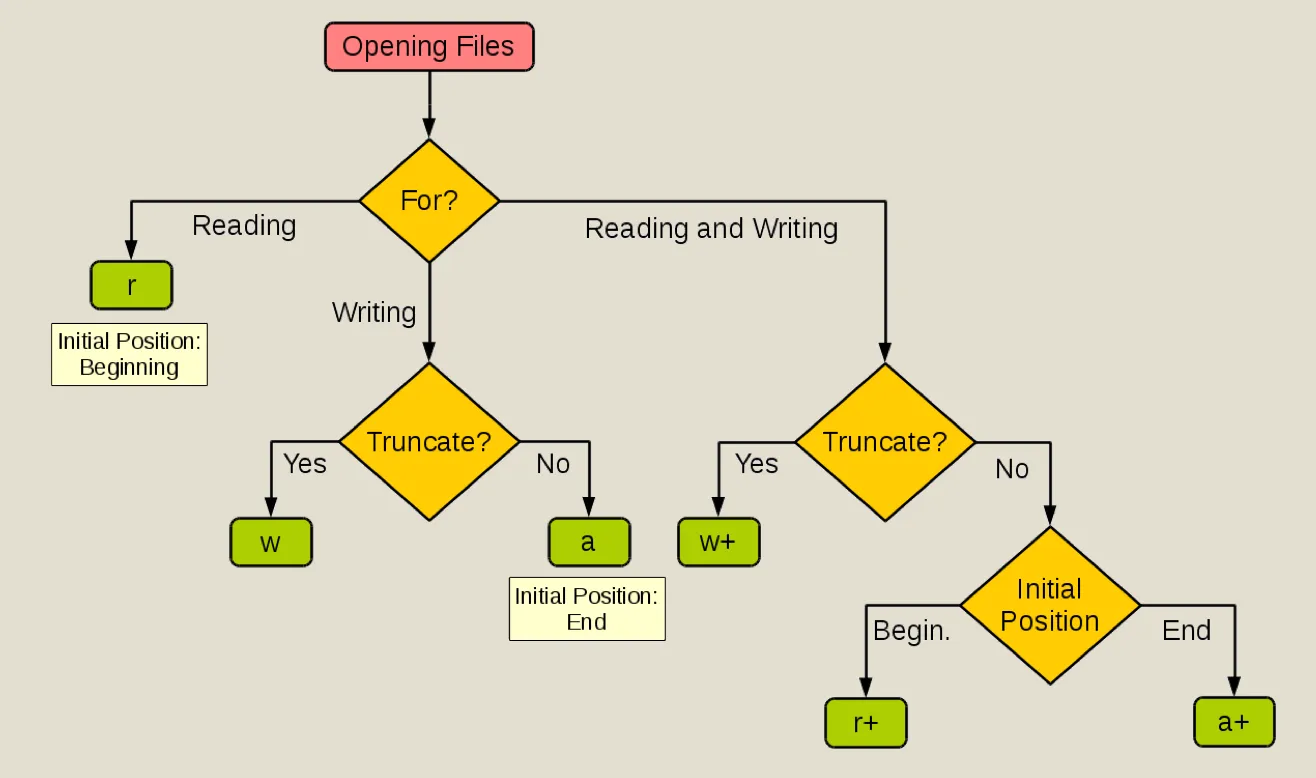
readlines() 方法读取文件所有行，返回一个列表；read() 方法读取整个文件内容，返回一个字符串，可以制定读入的字节数。
但是 open() 会保留行尾换行，如果需要去掉行尾换行符，可以使用 strip() 方法。
文件写入：write()方法
上下文管理器：with 语句用于自动管理资源，确保文件在使用后正确关闭。

8 Python的异常处理#

python 异常处理流程：当有异常出现时，它会使当前的进程停止，并且将异常传递给调用进程，直到异常被处理为止。
可以使用 try-except 语句捕获异常，except 块可以指定捕获特定类型的异常。
主动触发异常：raise exceptions
try 语句可以选 finally 子句，该子句无论如何都会执行，通常用于释放外部资源

9 OS模块#

9.1 文件管理#

创建目录：os.mkdir(path)，创建多级子目录：os.makedirs(path)。
删除目录：os.remove(path)
遍历目录：for root, dirs, files in os.walk(path)，返回目录树的根目录、子目录列表和文件列表。
文件重命名：os.rename(src, dst)
高级文件操作（复制、压缩）放在 shutil 模块中。

10 第二次作业讲评#

is_alpha 用于判断字符串是否只包含字母

类型化编程#

Python 是一种面向对象的编程语言，类是其核心概念之一。通过类，可以创建自定义数据类型，封装数据和方法，实现继承和多态等面向对象的特性。

1 类的定义与实例化#

类是对象的蓝图，定义了对象的属性和方法。通过关键字 class 定义类，实例化类可以创建具体的对象。

2 类的基本结构#

一个类通常包含以下部分：

类名：遵循大驼峰命名法
属性：描述对象的状态
方法：定义对象的行为，对象方法的形参通常包括 self，表示实例自身，而且必须位于最前面

2.1 self参数、实例属性#

self 本质是一个占位符，用于显示的指明实例的私有名字空间。被__new__()方法赋值
函数 __str__() 返回实例的字符串表示，通常用于打印输出。

3 类实例、类属性#

类属性由该类和所有派生的对象实例共享
实例属性不会修改类属性，但是修改类属性会影响所有实例

3.1 property 装饰器定义只读属性#

使用 @property 装饰器可以将方法转换为只读属性，避免直接访问实例属性。
被@PROPERT Y 装饰的方法通常用作属性的GETTER 方法，即它返回属性的值。如果希望外部代码能够设置属性的值，可以使用@属性名.SETTER 装饰器来定义一个SETTER 方法。在这个方法中，我们可以对输入值进行验证，然后将其赋值给私有属性。

3.2 序列对象的内置方法#

__iter__()：返回迭代器对象，支持 for 循环。
__next__()：返回下一个元素，支持迭代器协议。
__reversed__()：返回反向迭代器，支持反向遍历。

属性的设置

__len__()：返回对象长度，支持 len() 函数。
__contains__()：实现成员测试，支持 in 操作符。

4 可调用对象#

callable() 函数用于检查对象是否可调用（如函数、类实例等）。
普通数据、普通对象实例返回 False；函数、类实例返回 True。
实现 __call__() 方法可以使类实例变为可调用对象。
基于类实现的装饰器：必须实现 call 和 init两个内置函数。 init ：接收被装饰函数f，call（）：保证是可调用对象，同时在内部实现对输入函数的装饰逻辑
每次调用，就是相当于调用了类的 __call__() 方法，传入参数和关键字参数。

5 继承与多态#

5.1 继承#

继承允许一个类继承另一个类的属性和方法，被继承的类称为父类（基类），继承的类称为子类（派生类）。子类可以扩展或重写父类的方法。

5.2 构造函数#

如果要传参，就要使用到构造函数，

经典类的写法：父类.__init__(self, 参数1, 参数2)
新式类的写法：super(子类, self).__init__(参数1, 参数2)

5.3 方法继承#

C3 线性继承，mro 继承

5.4 静态方法#

静态方法使用 @staticmethod 装饰器定义，不需要访问实例或类属性。适用于不需要访问实例或类状态的方法。
静态方法设定为恒定的当前运行环境，类方法的运算环境可以随着继承关系而进化
静态方法由于不使用相对引用来标定参数因此不会随着继承到新环境而改变运算逻辑
类方法由cls参数自动带入类的环境引用，因此会随着继承到新环境而改变运算逻辑

5.5 多态#

多态是指不同类的对象可以对同一方法做出不同响应的特性。通过继承和方法重写实现多态。

编程模式-并发#

Python 并发编程允许程序同时执行多个任务，提高效率和响应性。根据实现方式和适用场景，Python 提供了多种并发编程模型。

1 并行与并发#

并发是指多个任务在同一时间段内交替执行，而并行是指多个任务在同一时刻同时执行。多线程、协程是并发，多进程是并行。

2 `name` 属性#

模块（.py文件）创建之初会自动加载一些内建变量

3 Python设计模式#

3.1 策略模式#

三部分

上下文（Context）：使用策略的类，持有对策略接口的引用。
策略接口（Strategy）：定义一组算法的接口。
具体策略（Concrete Strategy）：实现策略接口的具体算法。

3.2 单例模式#

保证一个类仅有一个实例，并提供一个全局访问点。

重写 __new__() 方法，确保类只能创建一个实例。

3.3 观察者模式#

多使用一种注册-通知-撤销注册的形式 Observer）将自己注册到被观察对象（Subject）中，被观察对象将观察者存放在一个容器（Container）里

3.4 工厂模式#

抽象类：抽象类是被继承的，不能直接实例化
用 abc.abstractmethod 装饰器定义抽象方法，子类必须实现。

4 并发编程#

多进程：进程通讯机制
多线程：线程锁与同步
协程-时间轮转机制：单线程分时任务处理
并行：多核 CPU 不同核上跑的两个进程，两个计算流在时间上重叠
并发：单核 CPU 跑的两个进程，两个计算流在时间上交替执行

5 线程（Threading）#

线程：调度执行的最小单元
- 每个线程运行在单一进程中
- 一个进程中可以有多个线程
线程上下文
- 程序计数器、通用目的寄存器、浮点寄存器、条件码
- 线程 ID、栈、栈指针
线程间可以共享进程空间的公有数据
多进程：程序之间不共享内存，使用虚拟地址映射保证资源独立
- 优点：一个进程挂了不影响别的进程
- 缺点：进程间通信（IPC）开销大，创建和销毁进程开销大
多线程：
- 优点：上下文切换效率高，线程之间信息共享和通信方便
- 缺点：一个线程挂了会使整个进程挂掉，操作全局变量需要锁机制
线程锁机制：多个逻辑控制流同时读写共享的资源时，需要加入锁机制
p.start() 启动线程，p.join() 等待线程结束。
进程池：固定数量的进程，有任务要处理就拿一个进城来处理任务
两个进程传递消息，可以使用 Pipe()，多个进城共享消息或数据可以使用 Queue()，
消息队列的常见应用：生产者-消费者

6 第四次作业讲评#

变量引用的特点：闭包中的内部函数不会拷贝外部变量的值，而是引用这个变量，如果变量修改，内部函数看到的是修改后的值
yield from 用于委托生成器，可以将一个生成器的输出直接传递给另一个生成器。

线程-协程-网络编程#

Python 提供了丰富的并发和网络编程模型，通过线程、协程和网络库实现高效的多任务处理和网络通信。

1 多线程资源锁#

线程间可以共享全局变量，可以用锁机制来协调多线程的运行在 CPython 中由于全局解释器锁 GIL 的存在，多核 CPU 无法提升效率，可以选择没有 GIL 的 Python 实现（如 IPython）

2 协程（Coroutine）#

本质上是一个可被异步唤醒的函数，存在自阻塞操作的被动服务函数，存在发出调用操作并等待调用返回才继续执行的主动客户方，协程的调度由用户程序（而非系统内核）自己来控制

2.1 生成器函数被动响应#

在函数里定义 a = yield b，利用 send 方法发送一个值，会被 a 接受，启用 next 的时候返回 b（next 其实会发送 None）

2.2 异常注入与 throw方法#

在生成器函数中，可以使用 throw 方法向协程发送异常，协程可以捕获并处理这些异常。

2.3 回调函数#

在函数中调用一个作为参数传入的函数

2.4 yield from 与协程嵌套#

yield from“ 是一个在Python协程（coroutine）中使用的表达式。它的意思是唤醒某个生成器“产生”值，并且在那个地方暂停执行，等待被唤醒生成器（协程）产生后继续执行。
用 await 代替 yield from ，异步 awaitable object 要使用 async def 定义异步函数。

3 正则表达式#

\, ^, \d, \w, \s、*、+、?、{m,n},
re.match()：从字符串开头匹配正则表达式。
re.search()：在字符串中搜索正则表达式。
re.findall()：返回所有匹配的子串列表。
\A, \Z, ^, $, \b, \B
括号是分组，多个分组按左括号从左往右从 1 开始编号
电话号码：^\d{11}$
邮箱：^[a-zA-Z0-9.]+@[a-zA-Z0-9.]+$
在量词后面加上 ? 可以变成非贪婪模式，匹配尽可能少的字符

4 网络编程基础#

连网的计算机根据其提供的功能将之区分为客户机或服务器（C/S）
通信协议：计算机之间以及计算机与设备之间进行数据交换而遵守的规则、标准或约定
- TCP/IP（在互联网上采用），IEEE802.3以太网协议（局域网），IEEE902.11 （无线局域网，WIFI）
网络通信识别的基本方案：
- 服务器监听特定的端口：如8080
- 得到请求后建立数据链路（远程I/O strem）
- 启动阻塞式通讯（TCP）
C/S 架构与 B/S 架构
- C/S（Client/Server）：12306 APP 购票，客户端和服务器端直接通信，适用于需要高性能和实时交互的应用。
- B/S（Browser/Server）：12306 网页购票，浏览器作为客户端，通过 HTTP 协议与服务器通信，适用于 Web 应用。
HTTP 协议：超文本协议

NumPy#

1 初始化#

2 reshape#

3 运算#

add, subtract, multiply, divide, power 等函数用于逐元素的运算
np.concatenate() 默认沿着第一个轴连接数组，axis=0 表示按行连接，axis=1 表示按列连接。
- vstack：沿着 axis =0
- stack：新的维度
sort（）：
- 默认为 -1，最后一个轴
- 否则指定哪个按哪个
- axis =None 展平之后排

4 广播#

维度有一个对上了，另一个是 1 就可以
向量乘法：
- 最常用 np.dot 对于一维相当于点积，对于二维相当于矩阵乘法 matmul 或者 @ ，否则就是沿着 a 的最后一个轴与 b 的倒数第二个进行点积
- vdot 是绝对的向量点乘
- inner 内积，否则就是沿着最后一个轴的内积和
切片只是一个视图，不会复制数据，改变切片会修改元数据，
- 拷贝可以用 copy 或者 take
- 省略号会省略其他维度
- 切片参数如果是一个 list，就采用高级索引模式
- 通过下标元组得到的是一个副本
- 生成表达式也可以作为索引

5 画图#

6 线性代数包#

计算 Bx = C 的解，使用 np.linalg.solve(B, C) 或者 np.linalg.inv(B)@C
线性空间变换可以用变换矩阵直接点乘

7 特征值与特征向量#

SIMD（Single Instruction Multiple Data）指单条指令对多数据进行并行处理，适用于向量化操作。

8 Kmeans 聚类#

8.1 步骤#

随机选择 K 个初始聚类中心。
将每个数据点分配到最近的聚类中心。
更新每个聚类中心为其所属数据点的均值。
重复步骤 2 和 3，直到聚类中心不再变化或达到最大迭代次数。
返回最终的聚类中心和每个数据点的聚类标签。

8.2 意义#

Kmeans 会收敛到局部最优解
算法复杂度为 O(n * k * i)，其中 n 是数据点数量，k 是聚类数量，i 是迭代次数。
本质是一种贪心算法
需要预先指定 k 值和初始划分
VQ 下平方和误差最小

8.3 改进方案#

确定 K 值：使用肘部法则（Elbow Method）或轮廓系数（Silhouette Coefficient）。
初始种子选定

8.4 质量评价#

聚类的纯度：分出的结果中占比最高的类别所占的比例

P(S_{r}) = \frac{1}{n_{r}}\max (n_{r}^{i})

聚类结果的纯度：所有聚类中“最多类别数量”之和 ÷ 全数据量

P(S_{r}) = \sum\limits_{r=1}^{k} \frac{n_{r}}{n}P(S_{r})

F 值：准确率和召回率的调和平均数

\begin{aligned} P(i, r) &= \frac{n_{r}^{i}}{n_{r}} , R(i, r) = \frac{n_{r}^{i}}{n_{i}} \\ f(i, r) &= \frac{2 \cdot P(i, r) \cdot R(i, r)}{P(i, r) + R(i, r)}\\ F &= \sum\limits_{i}\max f(i,r) \end{aligned}

Numpy 进阶#

1 向量范数#

L1 范数（曼哈顿距离）：向量元素绝对值之和。
L2 范数（欧几里得距离）：向量元素平方和的平方根。
无穷范数（切比雪夫距离）：向量元素绝对值的最大值。
分别用 np.linalg.norm(x, ord=1)、np.linalg.norm(x, ord=2)、np.linalg.norm(x, ord=np.inf) 计算。
矩阵范数
- Frobenius 范数：矩阵元素平方和的平方根。np.linalg.norm(A, 'fro')
- 谱范数：矩阵的最大奇异值。np.linalg.norm(A, 2)
- 1-范数：矩阵每列元素绝对值之和的最大值。np.linalg.norm(A, 1)
- ∞-范数：矩阵每行元素绝对值之和的最大值。np.np.linalg.norm(A, np.inf)
中心化：减去列均值 A - A.mean(axis=0)，使得每列均值为 0。
正规化：使用 Frobenius 范数 A / np.linalg.norm(A, 'fro')，使得矩阵的 Frobenius 范数为 1。
布尔下标
布尔下标可以用于筛选满足条件的元素，返回一个布尔数组，True 表示满足条件，False 表示不满足。
np.where(condition, a, b) 返回满足条件的元素对应的索引位置，a 和 b 分别表示满足和不满足条件时的值。
np.clip(x, a_min, a_max) 用于将数组 x 中的元素限制在 [a_min, a_max] 范围内。

2 数据特征分析#

分布的信息量

H = -(p\log p+ q\log q)

编码系统的信息量

H(U) = E[-\log p_{i}]

2元编码系统均匀分布的信息熵定义为 1bit 4 元的可以算出是 2 bit 一个特征分布的方差越大，信息量越高

3 特征空间的正交化、标准化#

中心化

sample = np.random.normal(loc = 2, scale =1, sizs=(6,2))
sample -= sample.mean(axis=0)
std = sample / sample.std(axis=0)

plaintext

z-score 标准化

z = \frac{x - \mu}{\sigma}

4 特征值与特征空间#

eigVals, eigVecs = np.linalg.eig(A.T @ A)

plaintext

5 PCA#

特征值的能量占比= 特征值/特征值之和
cum_var_exp = np.cumsum(var_exp) 计算累计能量占比。
目标：降维的同时保留大部分信息
PCA 的作用包括：
- 降维、去噪、正交化

6 HITS#

一种用于网页排序的经典算法，由 Jon Kleinberg 提出。它通过分析网页之间的链接关系，将网页分为两类：

Hub 页面：指向许多高质量 Authority 页面的页面。
Authority 页面：被许多高质量 Hub 页面指向的页面。 HITS 算法的核心思想是 Hub 和 Authority 之间的相互增强关系：
一个好的 Hub 页面会指向许多好的 Authority 页面。
一个好的 Authority 页面会被许多好的 Hub 页面指向。

计算流程：

定义两个向量
1. Authority 向量 a：表示每个页面作为 Authority 的重要性。
2. Hub 向量 h：表示每个页面作为 Hub 的重要性。
更新规则
1. Authority 更新：每个页面的 Authority 分数等于所有指向它的 Hub 页面分数之和。
2. Hub 更新：每个页面的 Hub 分数等于它指向的所有 Authority 页面分数之和。
归一化：每次迭代后，对 Authority 和 Hub 向量进行归一化，防止数值爆炸。
收敛

7 SVD 分解与特征分解#

$N*M$ 的矩阵 X，rank 为 r，可以分解为三个矩阵的乘积：

X = U_{N*r} \Sigma_{r*r} V_{M*r}^T

奇异值分解的基本流程

\begin{aligned} v_{1}&= \arg \max_{|v_1|=1} \|Xv_{1}\|_{2}^{2} \\ v_{2}&= \arg \max_{|v_2|=1, v_2 \perp v_1} \|Xv_{2}\|_{2}^{2} \\ \cdots\\ v_{r}&= \arg \max_{|v_r|=1, v_r \perp v_1, \cdots, v_{r-1}} \|Xv_{r}\|_{2}^{2} \\ \end{aligned}

使用 U, s, VT = np.linalg.svd(X) 计算奇异值分解，其中 U 是左奇异向量矩阵，s 是奇异值向量（一维，可以使用np.fill_diagonal(Sigma, s)，VT 是右奇异向量矩阵的转置。最后选取 Sigma 的前 k 列

特征分解与主成分分析的应用场景

都会要求产生一组正交基
主成分分析：把样本投影到新的特征空间
- 特征工程（检索、聚类）、数据降噪、数据压缩
特征分解（SDV）：样本集被分解为 参数*特征 的线性表达
- 文档话题模型（主题分析）
- 隐含语意挖掘（词义泛化、协同过滤）降维后乘回矩阵
- 检索、聚类：也需要把样本投到新的特征空间
- 特征分析与压缩（GIF、jpg）：可以放松正交性约束

Pandas#

1 Series#

自动维护标号索引
支持下标和切片访问
也可以指定可哈希的索引（也可以是非连续的索引项）
loc 和 iloc 分别用于标签索引和位置索引

2 Dataframe#

初始化 df 使用字段名+数据序列
时间序列索引 dates = pd.date_range('20230101', periods=6)
排序：df.sort_values(by='column_name')，默认升序
df 列之间的运算自动进行索引键对齐/补缺
当列中出现 NaN 时，整数自动转为 float64，布尔值转为 object
isnull和 notnull 用于判断缺失值，fillna 用于填充缺失值，dropna 用于删除缺失值所在的行或列。

3 表的连接#

groupby：分组操作，得到 name，group 的 Series 或 Dataframe

3.1 index之间的计算#

类似于有序集合
&, |, ^ 分别表示交集、并集和差集

3.2 表的连接#

merge() 函数用于连接两个 DataFrame，自动按照公共字段为轴进行合并
on 参数指定连接的公共字段，how 参数指定连接方式（如 ‘inner’, ‘outer’, ‘left’, ‘right’，默认是 inner 当出现多对一的时候展开为多个），left_on 和 right_on 分别指定左侧和右侧 DataFrame 的连接字段。
连接使用 pd.concat() 函数，默认沿着行（axis=0）连接，可以通过 axis=1 沿着列连接。

文本信息处理#

1 距离度量#

杰卡德相似系数：

J(A, B) = \frac{|A \cap B|}{|A \cup B|}

杰卡德距离：

J_{\delta}(A, B) = 1 - J(A, B)

信息相关度：（表明两个随机变量是否比在其独立时更相关）

\begin{aligned} I(X;Y) &= \sum\limits_{x \in X} \sum\limits_{y \in Y} P(x, y) \log \frac{P(x, y)}{P(x) P(y)}\\ pmi(x;y) &= \log \frac{P(x, y)}{P(x) P(y)}\\ \end{aligned}

mean squared error（均方误差）：

RMSE = \sqrt{\frac{1}{n} \sum\limits_{i=1}^{n} (x_i - y_i)^2}

2 TF-IDF 权值#

tf-idf 权值计算公式

idf_{t}=\log \frac{N}{df_{t}}, w_{t,d}= tf_{t,d} \cdot idf_{t}

图像处理基础#

1 社区#

社区是指在图中具有较高密度的节点集合，社区检测旨在识别这些节点集合。社区发现的目标：

高内聚性：社区内节点之间的连接密度较高。
低耦合性：社区之间的连接密度较低。

1.1 社区发现的算法#

Louvain 算法：基于模块度优化的层次聚类算法，通过合并节点来最大化模块度。
- 模块度：$$ Q=\frac{1}{2m}\sum\limits_{i,j} \left( A_{ij} - \frac{k_i k_j}{2m} \right) \delta(c_i, c_j)
- 步骤：
  1. 初始化每个节点为独立社区。
  2. 迭代合并社区，选择合并后模块度最大的社区对。
  3. 重复迭代直到模块度不再提高。
Girvan-Newman 算法：基于边介数的算法，通过逐步移除边来发现社区。
- 边介数： $B(e)=\sum\limits_{s \neq t \neq e} \frac{\sigma_{st}(e)}{\sigma_{st}}$
  - 步骤：
    1. 计算所有边的介数。
    2. 移除介数最大的边。
    3. 重复步骤 1 和 2，直到图被分割成多个连通分量。
标签传播算法（Label Propagation Algorithm, LPA）：基于节点标签传播的算法。
- 步骤：
  1. 初始化每个节点的标签为其自身。
  2. 在每次迭代中，每个节点将其标签更改为其邻居中最常见的标签。
  3. 重复迭代直到标签不再变化。

2 图嵌入#

图嵌入是一种将图结构数据（节点、边、图整体）映射到低维向量空间的技术，同时保留原始图的拓扑结构、节点属性和其他关键信息。其核心目标是解决图数据的高维稀疏性和复杂关系表示问题，使图数据适用于传统机器学习模型（如分类、聚类、推荐等）

降维：
保留信息：
可计算性：算法：
基于 JACARD 关联的 PCA 近邻嵌入
DeepWalk：基于随机游走的节点嵌入方法，通过模拟随机游走生成节点序列，使用 Skip-Gram 模型学习节点向量。

3 图像处理#

3.1 局部不变特征检测和描述#

对遮挡、形变、类内差异稳定

寻找一组具有区分性的关键点在图像中检测具有稳定性和重复性的关键点（如角点）。
在每个关键点周围定义一个区域以关键点为中心划定一个固定或自适应大小的邻域区域。
提取并归一化该区域的内容获取区域内的像素特征并进行尺度、旋转或亮度归一化。
从归一化区域中计算局部描述子将区域特征编码成一个高维向量表示（如 SIFT、ORB）。
匹配局部描述子通过相似度度量在不同图像中寻找最匹配的特征对。

图像特征提取与DCT#

1 视觉特征的核心问题#

图像特征提取需解决三大挑战：

尺度变化：同一物体在不同拍摄距离下的特征匹配。
旋转变化：物体旋转后仍需保持特征一致性。
光照变化：不同光照条件下的鲁棒识别。

2 SIFT算子（尺度不变特征变换）#

2.1 自动尺度选择#

目标：通过尺度空间（Scale Space）检测图像中具有尺度不变性的关键点。
方法：
- 高斯拉普拉斯变换（LOG）：通过计算图像的拉普拉斯算子与高斯核的卷积（即LOG），检测图像中的“Blob”（斑点）特征。公式为： $L_{xx}(\sigma) + L_{yy}(\sigma)$ 其中， $\sigma$ 表示高斯核的尺度参数。
- 高斯差（DOG）：用不同尺度的高斯核差分近似LOG，计算效率更高。公式为： $DOG = G(\sigma_1) * I - G(\sigma_2) * I \quad (\sigma_1 > \sigma_2)$ 通过构建高斯金字塔和DOG金字塔，检测不同尺度下的极值点（每个像素与同尺度8邻域及上下尺度各9邻域共26个点比较）。

2.2 关键点特征方向表达#

方向直方图计算：以关键点为中心，计算邻域像素的梯度方向分布，生成方向直方图。
主方向确定：选择直方图峰值对应的方向作为关键点的主方向，确保旋转不变性。
正则化：将关键点邻域旋转至主方向，实现方向归一化。

2.3 SIFT特征描述子#

特征向量构建：将关键点邻域划分为 (4 \times 4) 个单元格（Cell），每个单元格计算8个方向的梯度直方图，最终形成 (4 \times 4 \times 8 = 128) 维向量。
特性：对尺度、旋转、光照变化具有较强鲁棒性，广泛用于图像匹配、物体识别等。

3 HOG算子（方向梯度直方图）#

3.1 核心思想#

通过计算图像局部区域的梯度方向直方图构成特征，适用于行人检测、人脸识别等场景，但不具备旋转不变性。

3.2 2. 提取流程#

灰度化与Gamma校正：标准化颜色空间，减少光照影响。
梯度计算：计算每个像素的梯度大小和方向，捕获轮廓信息。
单元格划分：将图像划分为小单元格（如 (6 \times 6) 像素/Cell）。
梯度直方图统计：每个单元格内统计梯度方向的分布，生成Cell级特征。
块（Block）归一化：将多个Cell组成Block（如 (3 \times 3) 个Cell/Block），进行对比度均衡，增强特征鲁棒性。
特征串联：将所有Block的特征串联，形成图像的HOG特征向量。

3.3 3. 代码示例（OpenCV实现）#

import cv2
import numpy as np

# 预设HOG参数
winSize = (20, 20)
blockSize = (8, 8)
cellSize = (8, 8)
nbins = 9
hog = cv2.HOGDescriptor(winSize, blockSize, blockStride=(8,8), cellSize=cellSize, nbins=nbins)

# 提取特征
hog_descriptors = hog.compute(gray_image)

python

17 神经网络#

1 梯度消失#

梯度消失问题是指在反向传播过程中，梯度会随着网络层的增加而逐渐减小，甚至在后面的计算中变得非常接近于零。这会导致神经网络在训练时无法正确学习到数据的特征，从而影响模型的准确性和性能。

采用激活函数ReLU（Rectified Linear Unit）是一种常见方法，降低了单层拟合的非线性能力。
负边置为0可以对比PMI表达。这种架构更强调捕获正相关性。

2 Batch Normalization#

训练过程中，不断统计当前mini batch中激活值的均值和方差，并使用它们进行标准化，保证下一层输入的分布较为稳定

加速收敛速度，缓解梯度消失等

3 Dropout#

属于模型正则化可以避免单层模型有过强的特征捕获表达能力

4 pytorch#

autograd 机制

创建一个张量，并设置 requires_grad=True，表示需要对它求导。例如：x = torch.tensor([2.0], requires_grad=True)
使用该张量进行一系列数学运算，PyTorch 自动构建计算图。例如：y = x ** 2 + 3 * x
调用 y.backward() 启动反向传播，自动计算所有梯度。
通过 x.grad 查看张量的梯度值。
每次前向传播都会动态构建新的计算图，确保灵活性和调试友好性。

5 卷积神经网络#

手写体识别框架：

卷积层
激活层
池化层
全连接层
激活层损失函数的定义 `criterion = nn.CrossEntropyLoss() 优化器 optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9) 计算梯度、更新参数

loss.backward()  # 反向传播计算梯度
optimizer.step()  # 更新参数

plaintext

网络的优化：

训练过程优化
- optimizer 的选择：Adam
  - 与SGD的核心区别在于计算更新步长时，增加了分母：梯度平方累积和的平方根。此项能够累积各个参数gt,i的历史梯度平方，频繁更新的梯度，则累积的分母项逐渐偏大，那么更新的步长(stepsize)相对就会变小，而稀疏的梯度，则导致累积的分母项中对应值比较小，那么更新的步长则相对比较大。
  - 对梯度的一阶矩估计（First Moment Estimation，即梯度的均值）和二阶矩估计（Second Moment Estimation，即梯度的未中心化的方差）进行综合考虑，计算出更新步长。
  - 优点
    - 实现简单，计算高效，对内存需求少
    - 参数的更新不受梯度的伸缩变换影响
    - 超参数具有很好的解释性，且通常无需调整或仅需很少的微调
      - 更新的步长能够被限制在大致的范围内（初始学习率）
    - 能自然地实现步长退火过程（自动调整学习率）
    - 很适合应用于大规模的数据及参数的场景适用于不稳定目标函数
    - 适用于梯度稀疏或梯度存在很大噪声的问题
数据优化
- 标准化
- 数据增强
模型参数优化

评价指标

准确率：有多少比例正确
精准率：预测为正的当中有多少正确
召回率：正样本中有多少被预测为正
F1-score：精准率和召回率的调和平均数

6 RNN模型#

在 pytorch 中的实现：

定义网络结构
- forward 中要 combine input 和 hidden
设置样本集
采用序列循环模式进行训练
序列编码的每一个输出都是前驱序列的编码结果
序列编码本质上是一个时序过程，理论上应该有滑窗限制
在语言类问题的处理中常常借用语言的自然边界，如标点
RNN序列编码是一个2阶模型仿真n阶模型，必然弱于真n阶模型的编码能力

7 LSTM模型#

假设：

当前输入： $x_t$
上一个隐藏状态： $h_{t-1}$
上一个细胞状态： $C_{t-1}$

7.1 （1）遗忘门 — 决定丢弃多少旧信息#

f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f)

$\sigma$ 是 sigmoid 激活，输出在 0~1 之间，代表遗忘比例
0 表示“完全忘记”，1 表示“完全保留”

7.2 （2）输入门 — 决定写入多少新信息#

i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)

7.3 （3）生成候选记忆 — 新的候选内容#

\tilde{C}_t = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C)

7.4 （4）更新细胞状态 — 结合遗忘旧记忆和添加新记忆#

C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t

$\odot$ 表示元素乘（Hadamard积）
这一步就是“部分保留旧记忆 + 部分加入新记忆”

7.5 （5）输出门 — 决定隐藏状态输出什么#

o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o)

7.6 （6）计算隐藏状态#

h_t = o_t \odot \tanh(C_t)

神经网络生成模型#

1 Seq2Seq#

模型的基本框架

ht = Encoder(e(xt), ht-1)
st = Decoder(d(yt), st-1)
\hat yt=f(st)

plaintext

解决 seq2seq 效率问题的一种方法：teacher forcing 定长输入 \to 定长输出，多余的用空字符补齐

2 self-attention#

矩阵运算

Attention(Q, K, V) = softmax\left(\frac{QK^T}{\sqrt{d_k}}\right)V

数据类型#

1 基础数据类型#

1.1 数值类型#

1.2 布尔类型（Bool）#

1.3 python 中的对象#

2 序列类型#

2.1 列表（List）#

2.2 元组（Tuple）#

2.3 string#

2.4 迭代器#

2.5 set 集合#

2.6 字典（Dict）#

2.7 容器类#

2.8 列表生成式#

2.9 高阶函数#

3 第一次作业讲评#

函数编程#

1 对象拷贝机制#

2 名字绑定及引用计数#

3 函数的一般性质#

4 函数实现generator#

5 匿名函数（Lambda表达式）#

6 函数高阶使用技术#

6.1 可变参数列表#

6.2 嵌套函数#

6.3 函数装饰器#

7 文件操作#

8 Python的异常处理#

9 OS模块#

9.1 文件管理#

10 第二次作业讲评#

类型化编程#

1 类的定义与实例化#

2 类的基本结构#

2.1 self参数、实例属性#

3 类实例、类属性#

3.1 property 装饰器定义只读属性#

3.2 序列对象的内置方法#

4 可调用对象#

5 继承与多态#

5.1 继承#

5.2 构造函数#

5.3 方法继承#

5.4 静态方法#

5.5 多态#

编程模式-并发#

1 并行与并发#

2 __name__ 属性#

3 Python设计模式#

3.1 策略模式#

3.2 单例模式#

3.3 观察者模式#

3.4 工厂模式#

4 并发编程#

5 线程（Threading）#

6 第四次作业讲评#

线程-协程-网络编程#

1 多线程资源锁#

2 协程（Coroutine）#

2.1 生成器函数被动响应#

2.2 异常注入与 throw方法#

2.3 回调函数#

2.4 yield from 与协程嵌套#

3 正则表达式#

4 网络编程基础#

NumPy#

1 初始化#

2 reshape#

3 运算#

4 广播#

5 画图#

6 线性代数包#

7 特征值与特征向量#

8 Kmeans 聚类#

8.1 步骤#

8.2 意义#

8.3 改进方案#

8.4 质量评价#

Numpy 进阶#

2 `name` 属性#