绿皮书题目整理：Brain Teaser

问题简化#

1 海盗分金#

• 5 个海盗分 100 个金币
• 从两个海盗开始：两个人的时候，第一个人可以拿走全部；三个人的时候，为了争取最后一个人，第一个人会给他一个金币；四个人的时候，会给，为了争取倒数第二个人，第一个人会给他一个金币；五个人的时候，为了争取倒数第一个和倒数第二个，第一个人会给他一个金币；对于任意 $2n+1$ 个海盗，第一个人需要给 $3, 5,\cdots ,2n+1$ 个人每个人一个金币，偶数类似

2 老虎和羊#

• 100 只老虎和一只羊，老虎吃了羊也会变羊，每只老虎想吃羊但怕被吃
• 奇数吃，偶数不吃

逻辑推理#

1 渡河#

• ABCD 四个人渡河，只有一把火炬，每次至多两个人渡河，而且以速度慢的那个人为准，A 要 10min，B 要 5min，C 要 2min，D 要 1min。
• 关键是要知道，不能让 A 和 B 走回头路，而且 A 和 B 一起可以节省时间，所以最开始，C 和 D 去，C 或者 D 回来，A 和 B 过去，D 或者 C 回来接另一个人

2 生日问题#

• 生日可能是 3.4， 3.5， 3.8， 6.4， 6.7 9.1， 9.5 12.1， 12.2， 12.8 告诉了你月份，告诉了 C 日期。你说你不知道而且 C 也不知道。C 说现在知道了。A 说他也知道了

3 卡牌游戏#

• 52 张牌，依次拿两张牌，一红一黑就丢掉，两红给你，两黑给庄家，最后如果你剩的多，你就赢，否则你就输。你愿意以什么赔率玩？
• 你和庄家永远一样多。因为丢掉的牌永远是红和黑一样多，所以你的牌永远和庄家的牌一样多。

4 烧绳子#

• 两根绳子，每根绳子点燃需要 60min，点燃的速度不均匀。问你怎么用这两根绳子测量 45min。
• 同时开始烧。一根烧一头，一根烧两头，两头烧完了，代表 30min，接下来烧一头的另一头，烧完了就 15min

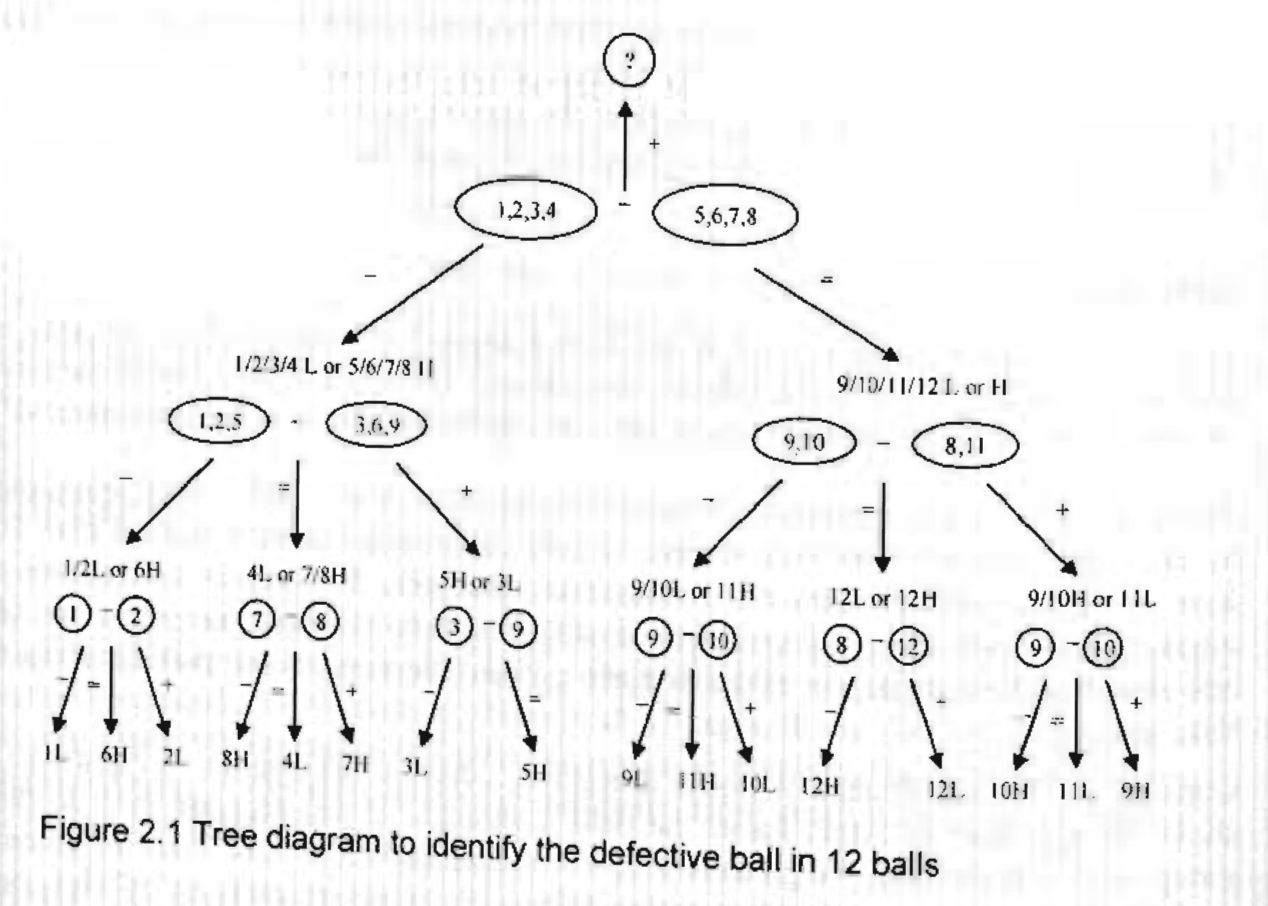
5 次品球#

• 12 个球，1 个次品球，重一点或者轻一点。用天平称三次，找出次品球。
• 

6 算尾0#

• 100！有多少个尾0
• 只要数 因子中 2 的个数和和 5 的个数，取小的那个

7 赛马#

• 25 匹马，5 条赛道，多少次比赛才能找出前 3 名
• 7 次

8 无穷序列#

• 如果 $x^{x^{x^{\dots}}} = 2$ ，$x$ 是多少？
• $x = \sqrt{2}$

打开思路#

1 装箱子#

• 53 块砖(1*1*4)，能不能装进 6 * 6 * 6 的箱子里
• 把箱子分成 27 个 2 * 2 * 2 的小箱子，砖可以放在小箱子里面，分别染上黑白色（13 黑，14 白），每个砖至少占一个白色的小箱子和一个黑色的小箱子，所以最后最多$13*4 = 52$块砖

2 日历骰子#

• 两个骰子，每个骰子 6 面，能不能用这两个骰子表示出 1-31 的日期
• 可以，首先两个都要有 $0, 1, 2$，然后剩下的平分掉

3 挑门#

• 两扇门，一扇通向死亡，一扇通向自由。门前都有守卫，死亡门前的守卫说谎，通向自由的守卫说真话。你可以问任意一个守卫一个问题，你该问什么？
• 问任意一个守卫，如果我问你另一扇门的守卫，他会说哪扇门通向自由

4 送消息#

• 你要给一个人送消息，每个人一把钥匙一把锁，你该怎么做？
• 先把消息锁起来，送过去，他再加上锁，再给你送回来，你再把你的锁打开，送过去

5 最后一个球#

• 20 个蓝球，14 个红球，每次取两个，取完不放回，两球颜色相同放一个蓝球，两球颜色不同放一个红球。问最后剩下的球是什么颜色？
• 最后剩下的球是蓝色，因为最后剩下的球的个数一定是奇数个，但是红球永远是偶数个

6 开关灯#

• 4 个房外开关，只有一个控制房内灯泡，问需要多少次才能找到开关
• 四个开关，需要两个二值变量确定，可以通过灯泡亮不亮和热不热来判断

7 量化工资#

• 八个人很想知道平均工资，不能直接告诉你工资。你该怎么做？
• 第一个人随机想一个随机数，加上自己的工资，传给下一个人，下一个人加上自己的工资，传给下一个人，最后第八个人传回给第一个人，第一个人减去自己的随机数即可

随机的应用#

1 硬币堆#

• 1000 个硬币，980个正面朝上，20 个反面朝上。你可以翻转任意数量的硬币，你看不见硬币的头反，你能不能分成两堆硬币，头一样多
• 假设分成两堆，第一堆 $n$ 个，其中 $m$ 个头向上，第二堆 $1000-n$ 个，其中 $20-m$ 个头向上。翻转第一堆的硬币，第一堆就有 $n-m$ 个头向上，只需保证 $n = 20$ 即可。

2 错标的袋子#

• 三个袋子，分别是苹果、橘子和 mix，但是都错标了。怎样最少次数取水果，确定标签？
• 先从 mix 里取一个水果，假设是苹果，那么 mix 就是苹果，橘子就是 mix，苹果就是橘子

3 智者#

• 50 个智者，随机进入一间房，房里有一个瓶子正着摆放，每个智者进房之后可以翻转瓶子或者什么都不做。智者们只能在最开始讨论一次，怎么确定最后是 50 个人都进入过房间了
• 只需要让一个人决定，每次他看到瓶子倒着了就翻转下来，其他人在第一次进入房子的时候如果瓶子正着就翻转一次，最后这个人就能知道有多少人进来过

序列求和#

1 钟表碎片#

• 钟表碎成了三片，每片的整数和相等，问怎么碎的
• 先算总和 78，找到 26，首先显然 5 6 7 8，然后 11 12 1 2，然后 3 4 9 10

2 消失的整数#

• 1-100 的整数，缺失两个整数
• 计算和、平方和然后计算解，这样的话时间复杂度是 $O(n)$，空间复杂度是 $O(1)$

3 找假包#

• 十个包，九个正常的，包里硬币十克，一个假包，包里硬币九克或者十一克，问怎么找出假包
• 编号，然后按照编号取硬币，称总重

4 玻璃球#

• 两个球，一百层楼，扔出去的高度高于 X 就碎，问最少多少次才能找到 X
• 实际上要反过来想，扔 N 次，最多能测试多少层楼：比如说在 M 楼第一扔如果失败了，那么接下来为了保证一定能找出来，至少要遍历 M-1 层楼，于是 N - 1 >= M-1，第一次最多在 N 楼；以此类推，第二次最多往上 N-1 楼；于是，N 次最多能到 (N+1)N/2 层楼。最后要满足 (N+1)N/2 >= 100，解出 N >= 14

鸽笼原理#

1 配袜子#

• 2 只红袜，20 只黄袜，31 只蓝袜，随手一抓，至少抓多少只保证有一双袜子
• 4 只

2 握手#

• 25 个人，是否至少有两个人握手的人数相等
• 只需要先把全不握过的人去掉，再把全握过的去掉，可以一下下搞，剩下假设 N 个人，既不全握过，也不是全不握过，每个人握手次数 1～N-1，于是至少两个人握手次数相等

3 我们好像在哪儿见过#

• 六个人里，要么有三个人互相认识，要么有三个互不认识的人
• 把你拿出来，剩下五个人，要么有多于三个人见过你，要么有多于三个人没见过你，分别讨论，如果有多于三个人见过你，他们中只要有人互相认识就可以了，否则的话说明这三个人互相不认识；如果有多于三个人没见过你，他们只要有人互相不认识就好了，否则的话就互相都认识

4 正方形上的蚂蚁#

• 边长为一的正方形，上面有 51 只蚂蚁，用一个半径为 1/7 的圆形玻璃杯，一定能找到一个位置盖住至少三只蚂蚁吗？
• 只需要把正方形看成 25 个边长为 1/5 的小正方形

5 假币二#

• 五个包，每个包 100 枚硬币，每个包的硬币可能是 9 10 或者 11 克，称几次能试出来
• 一个包只需要第一个包一个硬币，两个包需要第二个包三个硬币，因为 -4～4 才能满足 $3^2$ 个可能性，三个包需要第三个包九个硬币，四个包需要 第四个包27个硬币，五个包需要第五个包81个硬币

取模运算#

1 囚徒问题#

• 100 个囚徒，每个人一顶帽子，红色或者蓝色，囚徒们不能交流，帽子颜色是随机的，每次拉一个人出去猜自己的帽子颜色，如果猜对了就释放，问至少多少人猜对？
• 第一个人如果看到红色是奇数就猜红，否则猜蓝，其他人都可以根据第一个人的猜测和自己的帽子颜色来判断自己的帽子颜色
• 补充问题，如果帽子颜色是红黄蓝怎么办，只要把原来的奇偶判断换成将 红黄蓝判定为 0 1 2，计算求和取模

2 除9#

• 想出办法判断一个数是不是九的倍数
• 各数位数字相加，直到得到一位数，如果是 9 的倍数，那么得到的结果一定是 9
• 同理可以计算 11 的倍数 $a = (-1)^{n}a_{n} +(-1)^{n-1}a_{n-1}+\cdots +(-1)a_{1}+a_{0}$

3 变色龙的颜色#

• 13 只红色的变色龙，15 只绿色的，17 只蓝色的，每次两只不同色的变色龙相遇就会换个颜色，能否最后大家一个颜色
• 不可以，把红色，绿色，蓝色分别对应 0 1 2，每次相遇不改变总和 mod 3 的值，所以最后不可能全部变成同一种颜色

数学推导#

1 分硬币问题#

• 100 个硬币，分成两堆，分别有 $x, y$，计算 $xy$，再分别分成两堆$x_{1},x_{2}$和 $y_{1},y_{2}$，计算 $xy+x_{1}y_{1}+x_{2}y_{2}$，计算分到最后（每堆只有一个硬币）的和，并证明和分法无关
• 这是一个归纳法问题，从一枚硬币开始，每增加一枚硬币，都是加上原有的硬币个数，比如从 2 到 3 就是第三枚硬币依次加上了前两个硬币

2 巧克力棒问题#

• 一块巧克力棒，6 行 8 列 48 块，分成一个一个的小块，需要掰开几次
• 使用第二数学归纳法即可，最后结果是 $mn-1$

3 赛道#

• 环形赛道，随机放了 N 个油罐，刚好能跑完一圈，问空油车是否总能找到一个起点，沿途捡起油罐跑完一圈。
• 运用归纳法，实际上总可以找到一个 $x_i$ 大于 $y_i$，这时候就可以合并 $x_i$ 和 $x_{i+1}$
• 另一种解法比较好玩，你开另一辆满油的车跑一圈，碰到油罐就加油，加油前测量一下油量，油量最低的点就是你要的点（因为接下来花的油都不会超过你加的油，否则不是最低点）

反证法#

1 无理数#

• 证明 $\sqrt{2}$ 是无理数
• 很简单

2 彩虹帽#

• 七个囚徒，每个人一顶帽子，不允许交流，至少有一个人猜对了就放了，有没有必赢的策略
• 只需要把七种颜色编号为 0～6，每个人的猜测 $g_i$ 都满足$(g_{i}+ \sum\limits_{k\neq i}x_{k})\%7 = i$，这样的话如果每个人都不对，那么 $\sum\limits x_{k} \%7 \ne i,\forall i \in [0,6]$