抽象代数 UFD 理论

Note#

这一章节的所有内容，都是在说同一件事情，整数环 $\mathbb{Z}$ 在所有整环中，特别在哪里？按照这个逻辑，我们一步步研究整数环中的关键性质，最后一步步逼近它：

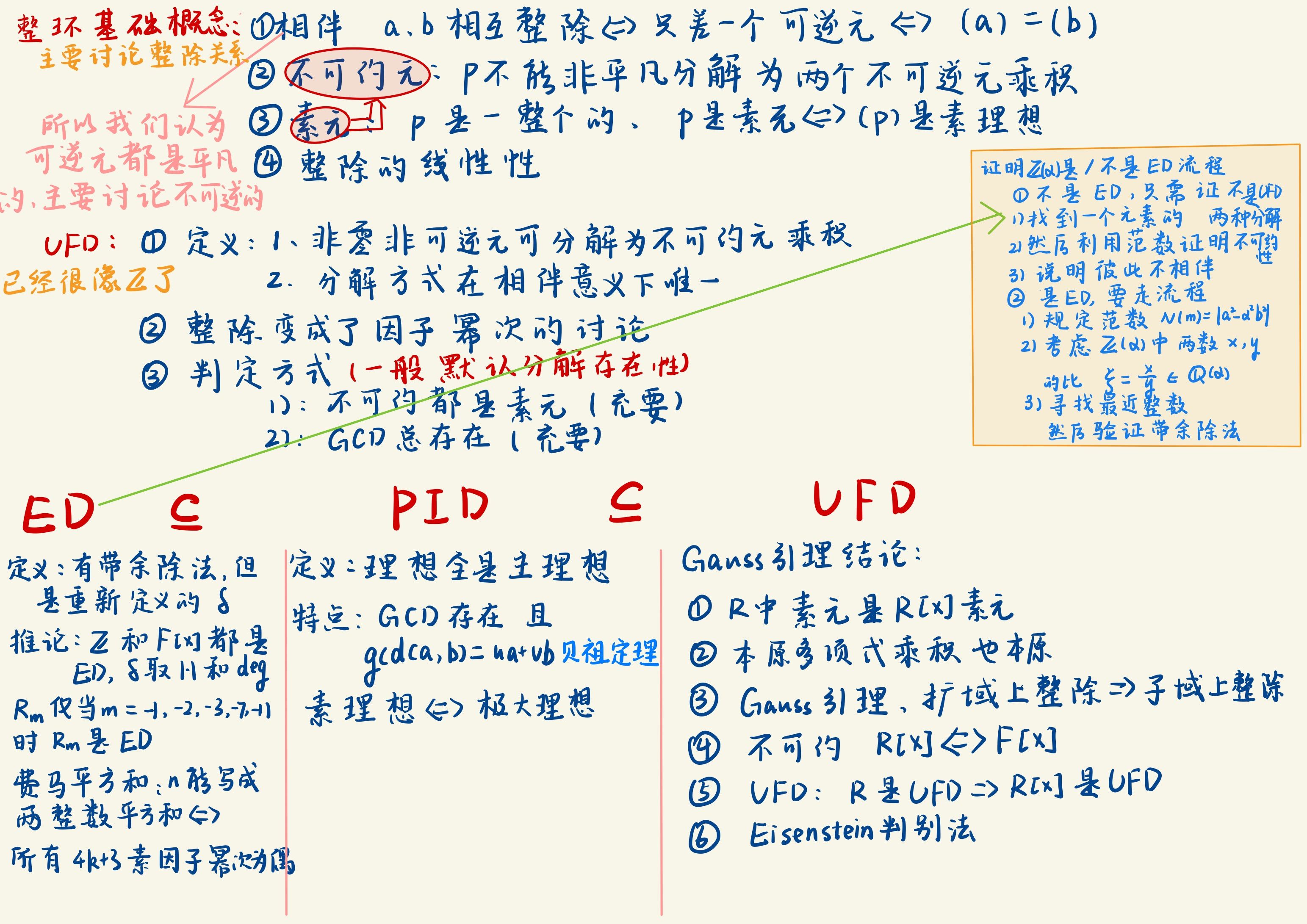
1. 整环：基本的加减乘系统。
2. Noether 环：保证分解过程会停止（存在性）。
3. UFD：保证分解结果只有一种（唯一性，算术基本定理）。
4. PID：保证GCD 具有线性组合形式（理想结构单一化）。
5. ED：保证能用算法（辗转相除）算出来。

整环中的整除、不可约元与素元#

整除：设 $R$ 为整环，对于 $a,b \in R$，若存在 $c \in R$ 使得 $b =ac$，就称 $a$ 整除 $b$，记作 $a \mid b$，这时也说 $b$ 是 $a$ 的倍元，$a$ 是 $b$ 的因子。 相伴：设 $R$ 为整环，$a,b \in R$，若 $a,b$ 可以互相整除，即 $a \mid b$ 且 $b \mid a$，则称 $a$ 与 $b$ 相伴，记作 $a \sim b$。

互素：设 $R$ 为整环，若 $a_{1},a_{2},\cdots,a_{n} \in R$ 的最大公因子是 $R$ 中的可逆元，则称 $a_{1},a_{2},\cdots,a_{n}$ 互素。

[!note]
只要 $R$ 中任意两个元素都有最大公因子，则 $R$ 中任意有限个元素都有最大公因子。 但是，并非所有整环中的元素都有最大公因子，例如 $F[X]$ 的子环 $R = \{ a_{0}+a_{1}X+a_{2}X^{2}+\cdots+a_{n}X^{n} \mid a_{0},a_{1},\cdots,a_{n} \in F, a_{1}=0 \}$ 中，$X^{2}$ 与 $X^{3}$ 就没有最大公因子。

不可约元：设 $R$ 为整环，$p \in R$，若 $p \ne 0$，且 $p$ 不是可逆元，并且 $p$ 不能写成 $p = ab$ 的形式，其中 $a,b \in R$ 都不是可逆元，则称 $p$ 是 $R$ 中的不可约元，否则称为可约元。 素元：设 $R$ 为整环，$p \in R$，若 $p \ne 0$，且 $p$ 不是可逆元，并且当 $p \mid ab$ 时，一定有 $p \mid a$ 或 $p \mid b$，则称 $p$ 是 $R$ 中的素元。 不可约元是在强调分解，素元是在强调其自身的性质 代数整数：首项系数为 $1$ 的整系数多项式的根成为代数整数。 证明素元的一种方式： $p$ 是 $\mathbb{Z}(\alpha)$ 的素元，当且仅当 $g(x)$ 模 $p$ 在 $\mathbb{Z}_{p}[x]$ 中不可约，其中 $g(x)$ 是 $\mathbb{Z}[x]$ 中的不可约元，且 $g(\alpha) = 0$, $\alpha \in \mathbb{C}$.

• 命题 5.1.1：设 $R$ 为整环，$a,b \in R$，则 $a$ 与 $b$ 相伴当且仅当存在可逆元 $u \in R$ 使得 $a = bu$，也当且仅当 $R$ 的主理想 $(a)$ 与 $(b)$ 相等。

• 命题 5.1.2：设 $R$ 是整环，$p \in R$，则 $p$ 在 $R$ 中不可约的充分必要条件是 $p\ne 0$，$p$ 不可逆，且当 $p = ab$ 时，则一定有 $p\mid a$ 或 $p \mid b$。

• 命题 5.1.3：设 $R$ 为整环，$p \in R$ 是素元当且仅当 $(p)$ 是 $R$ 的一个素理想。

• 定理 5.1.1：整环 $R$ 中的整除关系 $\mid$ 满足以下性质：

  1. 若 $a \mid b$ 且 $b \mid c$，则 $a \mid c$。
  2. 若 $a \mid b$ 且 $a \mid c$，则对任意 $r,s \in R$，有 $a \mid (rb + sc)$。

• 定理 5.1.2：整环中每个素元都是不可约元。

  • 反之不成立，例如在整环 $Z[\sqrt{-5}]$ 中，$6$ 有两种不同的不可约元分解形式 $6 = 2 \cdot 3 = (1 + \sqrt{-5})(1 - \sqrt{-5})$，其中的不可约元 $2,3,1 + \sqrt{-5},1 - \sqrt{-5}$ 都不是素元。

唯一因子分解整环#

唯一分解整环（UFD）：设 $R$ 为整环，且满足

1. $R$ 中每个非零非可逆元都能分解为不可约元的乘积；
2. 若 $a \in R$ 有两种不可约元分解形式 $a = p_{1}p_{2}\cdots p_{n} = q_{1}q_{2}\cdots q_{m}$，则 $n = m$，且经过重新排列后，对每个 $i$，都有 $p_{i} \sim q_{i}$， 则称 $R$ 为唯一因子分解整环。

• 命题 5.2.1：设 $R$ 是 UFD，$a,b \in R$ 均非零，又设 $a,b$ 有如下标准分解

$$a=u r_{1}^{m_{1}} r_{2}^{m_{2}} \cdots r_{s}^{m_{s}}, \quad b=v r_{1}^{n_{1}} r_{2}^{n_{2}} \cdots r_{s}^{n_{s}},$$

其中 $u,v$ 是可逆元，$r_{1},r_{2},\cdots,r_{s}$ 是互素的不可约元，且 $m_{i},n_{i} \ge 0$。则 $a\mid b$ 当且仅当对每个 $i$，都有 $m_{i} \le n_{i}$。

• 命题 5.2.2：设 $R$ 是 UFD，$a,b,c \in R$ 且 $a,b$ 互素，
  • 若 $a \mid bc$，则 $a \mid c$；
  • 若 $a \mid c$ 且 $b \mid c$，则 $ab \mid c$。
• 定理 5.2.1：设 $R$ 是整环，且满足 UFD 的条件 1，则 $R$ 是 UFD 的充分必要条件是 $R$ 中的每个不可约元都是素元。
  • 推论 5.2.1：设 $R$ 是整环，则 $R$ 为 UFD 当且仅当满足
    • $R$ 中每个非零非可逆元都能分解为不可约元的乘积；
    • $R$ 中每个不可约元都是素元。
  • 推论 5.2.2：设 $R$ 是整环，则 $R$ 为 UFD 当且仅当每个非零非可逆元 $a \in R$ 都是有限个素元的乘积。
• 定理 5.2.2：设 $R$ 是 UFD，则 $R$ 中任意两个元素都有最大公因子
• 定理 5.2.3：设整环 $R$ 中任意两个元素都有最大公因子，则 $R$ 的不可约元都是素元。
  • 推论 5.2.3：设整环 $R$ 中任意两个元素都有最大公因子，则 $R$ 为 UFD 当且仅当 $R$ 中任意两个元素都有最大公因子。

Noether 环和主理想整环#

Noether 环：设 $R$ 是交换环，若对任意的理想升链

$$J_{1} \subseteq J_{2} \subseteq J_{3} \subseteq \cdots$$

一定存在正整数 $n$，使得对所有 $m \ge n$，都有 $J_{m} = J_{n}$，则称 $R$ 为 Noether 环。

主理想整环（PID）：设 $R$ 是整环，若 $R$ 中的每个理想都是主理想，则称 $R$ 为主理想整环。 PID 都是 Noether 环

• 命题 5.3.1：设 $R$ 是主理想整环，则 $R$ 中任两个元素 $a,b$ 都有最大公因子 $d$，且存在 $u,v$，使得 $d = au + bv$。

• 定理 5.3.1：交换环 $R$ 是 Noether 环当且仅当 $R$ 中的每个理想都是有限生成的。

• 定理 5.3.2：Noether 整环中每个非零不可逆元都是有限个不可约元的乘积。

• 定理 5.3.3：设 $R$ 为主理想整环，$p \in R$，则下列陈述等价

  • $p$ 是 $R$ 中的不可约元；
  • $(p)$ 是 $R$ 中的极大理想；
  • $p$ 是 $R$ 中的素元；

• 定理 5.3.4：主理想整环是唯一因子分解整环。

Euclid 整环#

Euclid 整环：设 $R$ 是整环，令 $R^{*}=R \setminus \{0\}$，若存在映射 $\delta:R^{*} \to \mathbb{N}$，使得对任意 $a,b \in R$，$b \ne 0$，满足

$$a = qb+r$$

且 $r=0$ 或 $\delta(r) < \delta(b)$，则称 $R$ 为 Euclid 整环，记为 $ED$ ，映射 $\delta$ 称为 $R$ 上的 Euclid 函数。 整数环 $\mathbb{Z}$ 和一元多项式环 $F[x]$ 都是 Euclid 整环，其中 $\delta$ 分别取为 $\delta(a)=|a|$ 和 $\delta(f(x))=\deg f(x)$。 Gauss 素数：$R_{-1}=Z[i]$ 称为 Gauss 整环，其中的每一个元素 $a+bi$ （$a,b \in Z$）称为 Gauss 整数。为了区分，我们称整数环中的素数为有理素数，而 $Z[i]$ 中的素元称为 Gauss 素数。

• 命题 5.4.1：设 $m$ 是一个无平方因子的整数且 $m \ne 0,1$，定义 $R_{m}$ 为

$$R_{m} = \begin{cases} \{a + b \sqrt{m} \mid a,b \in \mathbb{Z}\}, & m \equiv 2,3 \pmod{4} \\ \{a + b \frac{1 + \sqrt{m}}{2} \mid a,b \in \mathbb{Z}\}, & m \equiv 1 \pmod{4} \end{cases}$$

则 $R_{m}$ 是 $\mathbb{Q}(\sqrt{ m })$ 中所有代数整数构成的集合。进一步地，$R_{m}$ 是域 $\mathbb{Q}(\sqrt{ m })$ 的子环，且是整环，称 $R_{m}$ 为 $\mathbb{Q}(\sqrt{ m })$ 的二次代数整数环

• 命题 5.4.2：设 $\alpha \in Z[i]$，则 $\alpha$ 为 $Gauss$ 素数当且仅当 $N(\alpha)$ 为有理素数，或者 $\alpha$ 的相伴元 $\pm \alpha,\pm i\alpha$ 中的一个为正有理素数，且该有理素数不是两个整数的平方和

• 定理 5.4.1：欧式环是主理想整环。

  • 推论 5.4.1：欧式环是唯一因子分解整环。
  • 事实上我们有 $\{ ED \} \subseteq \{ PID \} \subseteq \{ UFD \}$，而且这些包含都是真包含，比如 $Z[x]$ 是 UFD 但不是 PID，而 $Z\left[\frac{1+\sqrt{-19}}{2}\right]$ 是 PID 但不是 ED。

• 定理 5.4.2：当 $m<0$ 时，二次代数整数环 $R_{m}$ 是 Euclid 整环的充分必要条件是 $m=-1,-2,-3,-7,-11$。

• 定理 5.4.3：设正整数 $n\ge{2}$，则 $n$ 是两个整数的平方和当且仅当 $n$ 的每个形如 $4k+3$ 的素因子的幂次为偶数

UFD 上的多项式环#

本原多项式：设 $R$ 为 UFD，$f(x)\in R[x]$，若不存在 $R$ 中素元 $p$，使得 $p \mid a_{i}$ 对 $f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots+a_{1}x+a_{0}$ 中的每个系数 $a_{i}$ 都成立，则称 $f(x)$ 为 $R[x]$ 中的本原多项式。

• 命题 5.5.1：设 $R$ 为 UFD，$a,b \in R$，$f(x)\in R[x]$ 为本原多项式，若在 $R[x]$ 中有 $a\mid b f(x)$，则 $a \mid b$。

• 命题 5.5.2：设 $R$ 为 UFD，$F$ 为 $R$ 的分式域，$A$ 为一交换环，环同态 $\varphi: R \to A$ 诱导出的多项式环的环同态 $R[x]\to A[x]$ 仍记为 $\varphi$ 。设 $f(x)\in R[x]$ 首一，$\deg f(x)=n\ge 1$，且 $\varphi(f(x))$ 在 $A[x]$ 中无次数小于 $n$ 且大于 $0$ 的因子，则 $f(x)$ 在 $F[x]$ 中也不可约且为 $R[x]$ 的素元

• 定理 5.5.1：设 $R$ 为整环，$p$ 是 $R$ 中的素元，则 $p$ 也是多项式环 $R[x]$ 中的素元。

• 定理 5.5.2：设 $R$ 为 UFD，$f(x),g(x)\in R[x]$ 都是本原多项式，则它们的乘积 $f(x)g(x)$ 也是本原多项式。

• 定理 5.5.3（Gauss 引理）：设 $R$ 为 UFD，$F$ 是 $R$ 的分式域，$R[x]$ 和 $F[x]$ 是相应的多项式环

  • 设 $f(x),g(x)\in R[x]$，$g(x)$ 本原，且在 $F[x]$ 中 $g(x) \mid f(x)$，则在 $R[x]$ 中也有 $g(x) \mid f(x)$；
  • 设 $f(x)\in R[x]$，且存在 $g(x),h(x)\in F[x]$ 使得 $f(x) = g(x)h(x)$，则存在 $u \in F$ 使得 $ug(x),u^{-1}h(x) \in R[x]$。

• 定理 5.5.4：设 $R$ 为 UFD，$F$ 为 $R$ 的分式域，$f(x)\in R[x]$

  • 若 $f(x)=p \in R \setminus \{0\}$，则 $f(x)$ 在 $R[x]$ 中不可约当且仅当 $p$ 在 $R$ 中不可约；
  • 若 $\deg f(x)\ge1$，则 $f(x)$ 在 $R[x]$ 中不可约当且仅当 $f(x)$ 在 $F[x]$ 中不可约，且 $f(x)$ 是本原多项式。

• 定理 5.5.5：设 $R$ 为 UFD，则多项式环 $R[x]$ 也是 UFD。

  • 推论 5.5.1：设 $R$ 为 UFD，$n \ge 1$，则多项式环 $R[x_{1},x_{2},\cdots,x_{n}]$ 也是 UFD。

• 定理 5.5.6（Eisenstein 判别法）：设 $R$ 为 UFD，$p$ 是 $R$ 中的素元，$f(x) = a_{n}x^{n} + a_{n-1}x^{n-1} + \cdots + a_{1}x + a_{0} \in R[x]$，且满足

  • $p \nmid a_{n}$；
  • $p \mid a_{i}$，对 $i=0,1,2,\cdots,n-1$；
  • $p^{2} \nmid a_{0}$；
  • 则 $f(x)$ 在 $R[x]$ 中不可约。

• 定理 5.6.1（Hilbert 基本定理）：若 $R$ 是 Noether 环，则多项式环 $R[x]$ 也是 Noether 环。