抽象代数环理论

1 子环与同态#

自同态环：设 $G$ 为交换群，运算记为 $+$，用 $\operatorname{End}(G)$ 表示 $G$ 的全体自同态的集合。显然，$\operatorname{End}(G)$ 在映射的加法和复合运算下构成一个环，称之为交换群 $G$ 上的一个自同态环。 环直和：设 $R_{1},R_{2},\cdots,R _{n}$ 是环，令 $R = R_{1}\times R_{2}\times \cdots\times R _{n}$ 则，在逐点加法和乘法下，$R$ 是一个环，称之为环 $R_{1},R_{2},\cdots,R _{n}$ 的直和，记为 $R = R_{1}\oplus R_{2}\oplus \cdots\oplus R _{n}$。

幂等元：设 $R$ 为环，$a \in R$，若 $a^{2}=a$，则称 $a$ 为环 $R$ 的一个幂等元。 Boole 环：若环 $R$ 中的每个元素都是幂等元，则称环 $R$ 为一个 Boole 环。显然 boole 环是交换环。 除环：设 $R$ 为环，若 $R$ 中除零元外的每个元素都是可逆元，则称环 $R$ 为一个除环，或称为体。 整环：设 $R$ 为交换环，若 $R$ 中不存在零因子，即对任意 $a,b \in R$，$ab=0$ 蕴含 $a=0$ 或 $b=0$，则称环 $R$ 为一个整环。 整环和除环都有消去律，但是对于一般的环没有消去律 子环与扩环：设 $R$ 为环，$S$ 是 $R$ 的一个非空子集，且含有 $R$ 的乘法单位元 $1$. 若 $S$ 在 $R$ 的加法和乘法下还是环，则称 $S$ 为环 $R$ 的一个子环, 或称环 $R$ 为环 $S$ 的一个扩环。 容易看出，$\mathbb{Z}_{n}$ 的子环只有自身，因为 $\mathbb{Z}_{n}$ 的加法子群为由 $1$ 生成的循环群。类似地，整数环的子环也只有自身。 子域与扩域：设 $F$ 为域，若它的子环 $L$ 也是域，则称 $L$ 为域 $F$ 的一个子域，或称域 $F$ 为域 $L$ 的一个扩域。 四元除环：$\mathbb{H} = \{\begin{pmatrix}\alpha & \beta \\ -\bar{\beta} & \bar{\alpha}\end{pmatrix} |\alpha ,\beta \in \mathbb{C}\}$，显然 $\mathbb{H}$ 是 $\mathbb{R}$ 上的一个线性空间，且 $\mathbb{1}=\begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}, \mathbf{i}=\begin{pmatrix}i & 0 \\ 0 & -i\end{pmatrix}, \mathbf{j}=\begin{pmatrix}0 & 1 \\ -1 & 0\end{pmatrix}, \mathbf{k}=\begin{pmatrix}0 & i \\ i & 0\end{pmatrix}$ 是 $\mathbb{H}$ 的一组基，称 $\mathbb{H}$ 为四元数除环。 这是一个非交换除环，Wedderburn 定理说明，任意有限除环都是域，因此四元数除环是无限的。 令 $Q=\{ \pm \mathbb{1}, \pm \mathbf{i}, \pm \mathbf{j}, \pm \mathbf{k} \}$，则 $Q$ 在矩阵乘法下构成一个 8 阶的非交换群，称为四元数群。

环同态：设 $R,R'$ 为两个环，$\varphi: R\to R'$ 为映射，如果对于 $\varphi$ 保持加法和乘法运算，即对任意 $a,b \in R$，都有

$$\varphi(a+b)=\varphi(a)+\varphi(b), \varphi(ab)=\varphi(a)\varphi(b),$$

且 $\varphi(1_{R})=1_{R'}$，则称 $\varphi$ 为环到环 $R'$ 的一个环同态。同样地，若 $\varphi$ 是环同态且双射，则称 $\varphi$ 为环 $R$ 和环 $R'$ 之间的一个环同构，记为 $R \cong R'$。

• 命题 4.1.1：设 $S$ 为环 $R$ 的一个非空子集，则 $S$ 为 $R$ 的一个子环的充分必要条件是 $1\in S$ 且对任意 $a,b \in S$，都有 $a-b \in S$ 且 $ab \in S$。

  • 由此可以看出，环 $R$ 的最小子环一定是 $S_{0}=\{ n\cdot 1|n \in \mathbb{Z} \}$ 。

• 命题 4.1.2：设 $F$ 为域，$L \subset F$ 且 $\left| L \right|\ge 2$，则 $L$ 为 $F$ 的一个子域的充分必要条件是对任意 $a,b \in L,a\neq 0$，都有 $a-b \in L$ 且 $ab^{-1} \in L$。

• 定理 4.1.1（挖补定理）：设 $R$ 和 $S'$ 是两个环且 $R \cap S'=\emptyset$，$S$ 是 $R$ 的子环且 $S \cong S'$，则存在环 $R'$ 使得 $R' \cong R$ 且 $S'$ 是 $R'$ 的子环。

  • 类似于群论的挖补定理，证明也类似。

2 多项式环#

$R-$ 线性无关：设 $R$ 是交换环 $A$ 的一个子环，$x \in A$，称 $x$ 的幂次是 $R-$ 线性无关的，若对任意整数 $n\ge 0$，$R$ 中任意 $a_{0},a_{1},\cdots,a_{n}$，由

$$a_{0}+a_{1}x+a_{2}x^{2}+\cdots+a_{n}x^{n}=0$$

可推出

$$a_{0}=a_{1}=a_{2}=\cdots=a_{n}=0.$$

若 $x \in A$ 且 $x$ 的幂次是 $R-$ 线性相关的，则称 $x$ 为环 $R$ 上的一个不定元或未定元，也称为 $R$ 上的一个变元。

一元多项式：设 $R$ 是交换环 $A$ 的一个子环， $x \in A$ 是 $R$ 上的一个不变元。对任意 $n \in \mathbb{N},a_{0},a_{1},\cdots,a_{n}\in R$ ，称 $f(x)= \sum_{j =0}^{n}a_{j}x^{j}$ 为环 $R$ 上的一元多项式，记为 $f(x) \in R[x]$。其中 $a_{j}$ 称为多项式 $f(x)$ 的系数，若 $a_{n}\neq 0$，则 $n$ 称为多项式 $f(x)$ 的次数，记为 $\deg f(x)$，称首项系数为 $1$ 的多项式 $f(x)$ 为首一多项式。 多项式环：设 $R$ 是交换环 $A$ 的一个子环，$x \in A$ 是 $R$ 上的一个不变元，则由所有 $R$ 上一元多项式组成的集合记为 $R[x]$，显然是一个子环，称之为一元多项式环。 显然，多项式环 $R[x]$ 中 $f(x)=g(x)$ 当且仅当

$$\deg f(x)=\deg g(x)=n \text{ 且 } \forall 0\le j \le n, a_{j}=b_{j}$$

固定：设 $R$ 为交换环，$A$ 是 $R$ 的一个交换扩环，任取 $a\in A$，对任意 $f(x)=a_{0}+a_{1}x+\cdots+a_{n}x^{n}\in R[x]$，定义 $f(a)\in A$。这样 $\varphi_{a}:f(x)\mapsto f(a)$ 是 $R[x]$ 到 $A$ 的一个映射（称为固定映射）。显然，对任意 $r \in R$ 有 $\varphi_{a}(r)=r$，即 $\varphi_{a}$ 固定 $R$ 中的每个元素，这时也称 $\varphi_{a}$ 固定 $R$

• 命题 4.2.1：设 $f(x)$ 和 $g(x)$ 是交换环 $R$ 上的非零多项式，则：

  • 若 $\deg f(x)\ne\deg g(x)$，则 $f(x)+g(x)\ne 0$ 且 $\deg (f(x)+g(x))= \max\{\deg f(x),\deg g(x)\}$
  • 若 $\deg f(x)=\deg g(x)$，则 $\deg (f(x)+g(x))\le \deg f(x)$
  • $\deg (f(x)g(x))\le\deg f(x)+\deg g(x)$
  • 若 $R$ 为整环，则有 $f(x)g(x)\ne 0$，所以 $R[x]$ 也是整环，进一步地，$\deg (f(x)g(x))=\deg f(x)+\deg g(x)$

• 命题 4.2.2：设 $R$ 是整环，则 $U(R[x])=U(R)$ ，即 $R[x]$ 中的可逆元恰为 $R$ 中的可逆元。

  • $U(R)$ 表示环 $R$ 的可逆元全体。

• 命题 4.2.3：设 $\mathbb{F}$ 为域，$f(x)\in \mathbb{F}[x]$ 非零，$a\in \mathbb{F}$，则 $a$ 是 $f(x)$ 的根当且仅当存在 $g(x)\in \mathbb{F}[x]$ 使得 $f(x)=(x-a)g(x)$

• 命题 4.2.4：设 $\mathbb{F}$ 为域，$f(x)\in \mathbb{F}[x]$ 非零，则 $f(x)$ 在 $\mathbb{F}$ 中的不同根的个数不超过 $\deg f(x)$。

• 定理 4.2.1（带余除法定理）：设 $R$ 为交换环，$g(x)\in R[x]$，且满足 $g(x)$ 的首项系数为 $R$ 中的可逆元，则对 $\forall f(x)\in R[x]$，存在唯一的 $q(x),r(x)\in R[x]$ 满足 $f(x)=q(x)g(x)+r(x)$，且 $\deg r(x)< \deg g(x)$。

• 定理 4.2.2：设 $A$ 是 $R$ 中的一个交换扩环，$a\in A$，则映射 $\varphi_{a}: R[x]\to A$ 是一个固定 $R$ 的环同态。反之，每个固定 $R$ 的环同态 $\varphi: R[x]\to A$ 一定形如 $\varphi_{a}$，对某个 $a\in A$。

3 矩阵环#

全矩阵环：环 $R$ 上的 $n$ 阶方阵组成的集合记为 $M_{n}(R)$，在矩阵加法和乘法下是一个环，称之为环 $R$ 上的一个全矩阵环。全矩阵环中的可逆元称为可逆矩阵，无论 $R$ 是否交换，全矩阵环 $M_{n}(R)$ 都不交换。 三类初等变换：

• 交换两行（列）；$P_{ij}$

• 某行（列）乘以 $R$ 中的可逆元 $k$；$D_{i}(k)$

• 某行（列）加上另一行（列）的 $R$ 中的倍数；$S_{ij}(k)$

• 命题 4.3.4（Binet-Cauchy 公式）：设 $A$ 和 $B$ 分别是交换环 $R$ 上的 $m\times n$ 和 $n \times s$ 矩阵，并记 $C=AB$，则对任意 $1\le i_{1}<i_{2}< \cdots <i_{r}\le m$ 和 $1\le j_{1}<j_{2}< \cdots<j_{r}\le s$，都有

$$D_{C}\begin{pmatrix} i_{1},i_{2},\cdots,i_{r} \\ j_{1},j_{2},\cdots,j_{r} \end{pmatrix} =\sum_{1\le k_{1}<k_{2}< \cdots<k_{r}\le n}D_{A}\begin{pmatrix} i_{1},i_{2},\cdots,i_{r} \\ k_{1},k_{2},\cdots,k_{r} \end{pmatrix}D_{B}\begin{pmatrix} k_{1},k_{2},\cdots,k_{r} \\ j_{1},j_{2},\cdots,j_{r} \end{pmatrix}$$

4 理想与商环#

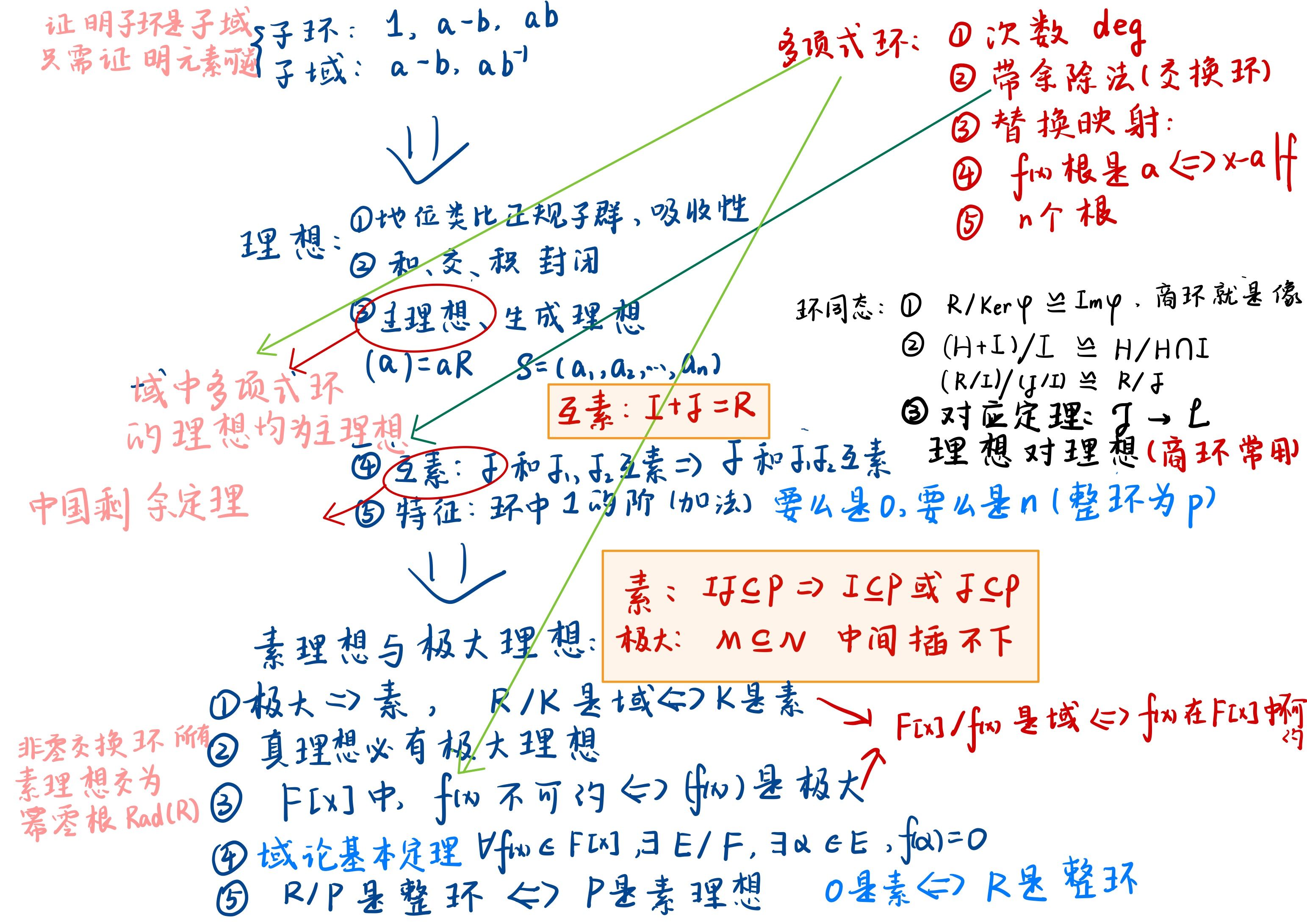
理想：设 $I$ 是环 $R$ 的非空子集，若 $I$ 是 $R$ 的加法子群，且对 $\forall r \in R,rI\subset I,Ir\subset I$，则称 $I$ 为环 $R$ 的一个理想。显然 $\{ 0 \}$ 和 $R$ 本身都是 $R$ 的理想，称为平凡理想；若 $R$ 只有平凡理想，称 $R$ 为单环。而且理想中不包含可逆元，因此若 $R$ 为除环，则 $R$ 只有平凡理想。

[!note] 理想和正规子群 理想的定义是从环同态核出发得到的，正如正规子群是从群同态核出发得到的一样

幂零根：交换环 $R$ 的幂零元全体构成 $R$ 的一个理想，称为环 $R$ 的幂零根，记为 $\operatorname{Rad}(R)$ 设 $R$ 为交换环，任取 $a \in R$，则 $aR$ 称为 $R$ 的理想，称其为元素 $a$ 生成的主理想，记为 $(a)$ 生成的理想：设 $S$ 是环 $R$ 的一个非空子集，则由 $S$ 中元素生成的环 $R$ 的最小理想称为由 $S$ 生成的理想，记为 $(S)$。如果 $S$ 是有限集，$S=\{a_{1},a_{2},\cdots,a_{n}\}$，则由 $S$ 生成的理想记为 $(a_{1},a_{2},\cdots,a_{n})$，称为由 $a_{1},a_{2},\cdots,a_{n}$ 生成的有限理想。特别地，若 $S = \{ a \}$，则称 $(a)$ 为主理想。 对于交换除环，$(a)$ 的形式为：

$$(a)=\{ra|r \in R\}$$

而对于一般的环，$(a)$ 的形式为：

$$(a)=\left\{\sum_{k=1}^{n}r_{k}ar'_{k}|r_{k},r'_{k}\in R,n\in \mathbb{N}\right\}$$

主理想环：设 $R$ 为环，若 $R$ 的每个理想都是主理想，则称环 $R$ 为一个主理想环。 商环：设 $I$ 是环 $R$ 的一个理想，定义在 $R$ 的加法商群 $R/I=\{a+I|a \in R\}$ 上的加法和乘法为

$$(a+I)+(b+I)=(a+b)+I$$ $$(a+I)(b+I)=ab+I$$

则 $R/I$ 在上述加法和乘法下构成一个环，称之为环 $R$ 关于理想 $I$ 的一个商环，其中单位元为 $1+I$。

• 命题 4.4.1：设 $I,J$ 都是环 $R$ 的理想，定义

$$\begin{align} I+J & =\{a+b|a\in I,b\in J\} \\ I \cap J & =\{a|a\in I \text{ 且 } a\in J\} \\ IJ & =\left\{\sum_{k=1}^{n}a_{k}b_{k}|a_{k}\in I,b_{k}\in J,n\in \mathbb{N}\right\} \end{align}$$

则 $I+J,I \cap J$ 和 $IJ$ 都是环 $R$ 的理想。

• 命题 4.4.2：设 $R$ 为交换环，$a_{1},a_{2},\cdots,a_{n}\in R$，则 $R$ 的由 $a_{1},a_{2},\cdots,a_{n}$ 生成的理想为

$$(a_{1},a_{2},\cdots,a_{n})=\{r_{1}a_{1}+r_{2}a_{2}+\cdots+r_{n}a_{n}|r_{i}\in R,1\le i \le n\}$$

进一步地，

$$(a_{1},a_{2},\cdots,a_{n})=a_{1}R+a_{2}R+\cdots+a_{n}R$$

• 定理 4.4.1：域 $F$ 上一元多项式环 $F[x]$ 的理想都是主理想，且每个非零理想 $(f(x))$ 的生成元 $f(x)$ 可以取为首一多项式。
  • 只需要考虑做带余除法即可。

5 环同态基本定理#

特征：设 $R$ 为环，令 $\varphi(k)=k\cdot 1,\forall k \in \mathbb{Z}$，则 $\varphi$ 是环 $\mathbb{Z}$ 到环 $R$ 的一个环同态，称其为特征同态。$\operatorname{Ker}\varphi$ 是 $\mathbb{Z}$ 的一个理想，因此存在唯一的非负整数 $n$ 使得 $\operatorname{Ker}\varphi=n\mathbb{Z}$，称 $n$ 为环 $R$ 的特征，记为 $\operatorname{char}R$。特别地，若 $\operatorname{Ker}\varphi=\{0\}$，则称环 $R$ 的特征为零。

互素：设 $I$ 和 $J$ 都是环 $R$ 的理想，若 $I+J=R$，则称理想 $I$ 和 $J$ 互素。

• 命题 4.5.1：若环 $R$ 的理想 $J$ 与 $J_{1},J_{2}$ 都互素，则 $J$ 与 $J_{1}J_{2}$ 也互素，从而 $J$ 与 $J_{1}\cap J_{2}$ 互素

• 定理 4.5.1（环同态基本定理）：设 $\varphi: R\to R'$ 是环 $R$ 到环 $R'$ 的一个环同态，令 $K = \operatorname{Ker}\varphi$，则

$$R/K \cong \operatorname{Im}\varphi$$

• 定理 4.5.2：设 $R$ 为环，则 $R$ 的特征要么为零，要么为某个正整数 $n$。进一步地，若 $\operatorname{char}R=0$，则 $R$ 有子环 $\mathbb{Z}$；若 $\operatorname{char}R=n>0$，则 $R$ 有子环 $\mathbb{Z}_{n}$。
• 定理 4.5.3：整环的特征为 $0$ 或素数
• 定理 4.5.4（第二同构定理）：设 $R$ 是环，$I$ 是 $R$ 的一个理想，$H$ 是环 $R$ 的一个子环，则 $H+I$ 是环 $R$ 的一个子环，$H\cap I$ 是环 $H$ 的一个理想，且

$$(H+I)/I \cong H/(H\cap I)$$

• 定理 4.5.5（第三同构定理）：设 $R$ 是环，$I$ 和 $J$ 都是环 $R$ 的理想，且 $I \subset J$，则 $J/I$ 是环 $R/I$ 的一个理想，且

$$(R/I)/(J/I) \cong R/J$$

• 定理 4.5.6（第三同构定理）：设 $R,R'$ 是环，$\varphi: R\to R'$ 是环同态，$J$ 是 $R$ 的一个理想，且 $\operatorname{Ker}\varphi \subset J$，则 $\varphi(J)$ 是环 $\varphi(R)$ 的一个理想，且

$$R/J \cong \varphi(R)/\varphi(J)$$

• 定理 4.5.7（对应定理）：设 $R,R'$ 是环，$\varphi: R\to R'$ 是环的满同态，令 $\mathcal{J}$ 为 $R$ 的所有包含 $\operatorname{Ker}\varphi$ 的理想组成的集合，$\mathcal{L}$ 是 $R'$ 的所有理想组成的集合，则
  • 若 $J \in \mathcal{J}$，则 $\varphi(J) \in \mathcal{L}$；若 $L\in \mathcal{L}$，则 $\varphi^{-1}(L) \in \mathcal{J}$；
  • 若 $J\in \mathcal{J}$，则 $\varphi ^{-1}(\varphi(J))=J$；若 $L\in \mathcal{L}$，则 $\varphi(\varphi^{-1}(L))=L$；
  • 映射 $J\mapsto \varphi(J)$ 是 $\mathcal{J}$ 到 $\mathcal{L}$ 的一个双射，其逆映射为 $L\mapsto \varphi^{-1}(L)$。
  • 若 $J \in \mathcal{J}$ ，则有环同构 $R/J \cong R'/\varphi(J)$。
• 定理 4.5.8（中国剩余定理）：设 $R$ 为环，$I_{1},I_{2},\cdots,I_{n}$ 是 $R$ 的两两互素的理想，则有环同构

$$R/(I_{1}\cap I_{2}\cap \cdots \cap I_{n}) \cong R/I_{1}\oplus R/I_{2}\oplus \cdots \oplus R/I_{n}$$

6 极大理想和素理想#

极大理想：设 $R$ 是环，$M$ 是 $R$ 的理想且 $M\ne R$，对 $R$ 的任意理想 $N$ ，若 $M\subset N$，必有 $N=M$ 或者 $N=R$，则称 $M$ 为环 $R$ 的一个极大理想。

素理想：设 $R$ 为环，$P$ 是 $R$ 的真理想，且对于 $R$ 的任意理想 $I$ 和 $J$ ，由 $IJ\subset P$ 可得到 $I\subset P$ 或者 $J\subset P$，则称 $P$ 为环 $R$ 的一个素理想。

• 命题 4.6.1：设 $F$ 是域，$f(x)\in F[x]$ 且 $\deg f(x)=2$ 或 $3$ ，则 $f(x)$ 在 $F[x]$ 中不可约当且仅当 $f(x)$ 在 $F$ 中无根

• 命题 4.6.2：设 $R$ 为环，则环 $R$ 的每个极大理想都是素理想。

• 定理 4.6.1：设 $R$ 是交换环，$K\ne R$ 是 $R$ 的理想，则 $R/K$ 是域当且仅当 $K$ 是 $R$ 的极大理想。

  • 推论 4.6.1：设 $R$ 是交换单环，则 $R$ 为域
  • 推论 4.6.2：设 $n$ 为非负整数，则 $\mathbb{Z}_{n}$ 为域当且仅当 $n$ 为素数。

• 定理 4.6.2：设 $R$ 为非零环，$I$ 为 $R$ 的理想且 $I\ne R$，则存在环 $R$ 的极大理想 $M$ 使得 $I \subset M$。

• 定理 4.6.3：设 $F$ 为域，$f(x)\in F[x]$ ，则 $(f(x))$ 是 $F[x]$ 的极大理想当且仅当 $f(x)$ 在 $F[x]$ 中不可约

• 定理 4.6.4：设 $F$ 是域，则商环 $F[x]/(f(x))$ 是域当且仅当 $f(x)$ 在 $F[x]$ 中不可约。

• 定理 4.6.5（Kronechker 定理，域论基本定理）：设 $F$ 为域，$f(x)\in F[x]$，$\deg f(x)\ge 1$，则存在 $F$ 的扩域 $E$ 使得 $f(x)$ 在 $E$ 中有根。

• 定理 4.6.6：设 $R$ 为非零交换环，$P$ 是 $R$ 的真理想，则下面陈述等价：

  • $P$ 是环 $R$ 的素理想；
  • 商环 $R/P$ 是整环。
  • $\forall a,b \in R$，若 $ab \in P$，则 $a \in P$ 或 $b \in P$。
  • 推论 4.6.3：设 $R$ 为非零交换环，则 $\{0\}$ 是环 $R$ 的素理想当且仅当 $R$ 是整环。

• 定理 4.6.7：设 $R$ 是非零交换环，则 $R$ 的所有素理想的交恰好是 $R$ 的幂零根 $\operatorname{Rad}(R)$

7 分式域域局部化#

整环的局部化：设 $R$ 为整环，考虑集合

$$R\times R\setminus \{0\}=\{(a,b)|a,b \in R,b\ne 0\}$$

在该集合上定义关系 $\sim$ 为 $(a,b)\sim (c,d)$ 当且仅当 $ad=bc$。容易验证 $\sim$ 是等价关系，记等价类为 $\frac{a}{b}$。则

$$F = \left\{\frac{a}{b}|a,b \in R,b\ne 0\right\}$$

在以下加法和乘法下构成一个域：

$$\frac{a}{b}+\frac{c}{d}=\frac{ad+bc}{bd}, \frac{a}{b}\cdot \frac{c}{d}=\frac{ac}{bd}$$

分母集：设 $R$ 为非零交换环，$D$ 是 $R$ 的一个子集，满足 $1\in D，0\not\in D$，$D$ 无零因子，且 $D$ 对乘法封闭，即对于 $a,b \in D$，$ab \in D$，则称 $D$ 为环 $R$ 的一个分母集。称

$$R_{D}=\left\{\frac{a}{b}|a \in R,b \in D\right\}$$

为 $R$ 关于分母集 $D$ 的局部化。

Laurent 多项式环：设 $R$ 为交换环，$x$ 是 $R$ 上的一个不定元，则由所有形如

$$f(x)=\sum_{j=m}^{n}a_{j}x^{j}$$

的多项式组成的集合记为 $R[x,x^{-1}]$，其中 $a_{j}\in R,m,n\in \mathbb{Z},m\le n$。在逐点加法和乘法下，$R[x,x^{-1}]$ 构成一个环，称之为环 $R$ 上的Laurent 多项式环。

• 定理 4.7.1：设 $R$ 为整环，$\sigma$ 为环 $R$ 到域 $K$ 的单同台，则存在唯一的域的单同态 $\pi: F\to K$ 使得 $\sigma=\pi f$